「住宅ローンの計算をしてみる」シリーズのパート4です。
この記事では、これまで導出してきた式に実際に数字を代入して、住宅ローンの返済シミュレーションをしてみようと思います。
↓ これまでの式の導出 ↓
住宅ローンの計算をしてみる – 元利均等返済
住宅ローンの計算をしてみる – 元金均等返済
Contents
計算を始める前に
例によって、必要な値を次のように置きます。
毎月の支払い時の残金 … $x$
毎月の支払い額 … $y$
毎月の支払い額の元本返済分 … $z$
毎月の支払い額の利子分 … $w$
毎月の利息(月利) … $α$
支払い回数 … $N$
シミュレーション条件
シミュレーションの条件はこんな感じで行います。
金利 : 1 %
返済期間 : 35 年
この条件から、借入総額 $X$、毎月の利息(月利) $α$、支払い回数 $N$ はすぐに求められます。
借入総額: $X =\,$$30000000$
毎月の利息(月利): $α = 1\,\%\div12ヶ月\,\fallingdotseq\,$ $0.083333333$
支払い回数: $N = 35年\times\,12ヶ月=\,$$420$
元利均等返済
まず元利均等返済について計算します。
毎月の支払い額
毎月の支払い額を求めます。
元利均等返済ではこれが定数となり、その値 $Y$ はこのように表せるのでした。
Y = \frac{αX(1+α)^N}{(1+α)^N – 1}
\end{align}
各数字を代入していきます。
\begin{align}
Y &= \frac{(0.083333333\times0.01)\times30000000\times(1+(0.083333333\times0.01))^{420}}{(1+(0.083333333\times0.01))^{420} – 1}\\[10pt]
&\fallingdotseq84685.710
\end{align}
※ $α$ の値 $0.083333333$ はパーセンテージなので、$0.01$ をかけてから計算しています(これ以下も同様)
利子合計
元利均等返済の利子合計
\sum_{k=1}^N w_k &= (X-\frac{Y}{α})\left\{ (1+α)^N – 1 \right\} + NY
\end{align}
に各数字を代入します。
\begin{align}
\sum_{k=1}^{420} w_k &= (30000000-\frac{84685.710}{(0.083333333\times0.01)})\\
&~~~~\times\left\{ (1+(0.083333333\times0.01))^{420} – 1 \right\} + 420\times84685.710\\[10pt]
&\fallingdotseq5567998.0
\end{align}
元金均等返済
次に元金均等返済について計算していきます。
毎月の元本支払い額
毎月の元本支払い額を求めます。
元金均等返済ではこれが定数となり、その値 $Z$ はこのように表せるのでした。
Z &= \frac{X}{N}
\end{align}
に各数字を代入します。
\begin{align}
Z &= \frac{30000000}{420}\\[10pt]
&\fallingdotseq71428.571
\end{align}
初月の支払い額
元金均等返済では毎月の支払い額が変わるので、ここでは初月の額をみてみます。
毎月の支払額は
y_n &= Z + α\left\{X – (n – 1)Z \right\}
\end{align}
であったので、初月は $n\,=\,1$ として、
\begin{align}
y_1 &= 71428.571 + (0.083333333\times0.01)\times\left\{30000000\,- (1 – 1)\times71428.571 \right\}\\[10pt]
&=96428.571
\end{align}
利子合計
元金均等返済の利子合計
\sum_{k=1}^N w_k &= \frac{1}{2}α\left\{-ZN^2 + (2X + Z)N\right\}\\
\end{align}
に各数字を代入すると
\begin{align}
\sum_{k=1}^{420} w_k &= \frac{1}{2}\times(0.083333333\times0.01)\\
&~~~~\times\left\{-71428.571\times{420}^2 + (2\times 30000000 + 71428.571)\times420\right\}\\[10pt]
&\fallingdotseq5262500.0
\end{align}
比較する
ここまでで計算した元利均等返済と元金均等返済の支払いについて比較してみます。
初回支払い額と利子の合計額を比べると次のようになります。
| 初回支払い額(円) | 利子合計(円) | |
|---|---|---|
| 元利均等返済 | 84,686 | 5,567,998 |
| 元金均等返済 | 96,429 | 5,262,500 |
元金均等返済では初回支払いの金額が約1.1万円も高くなっています。
しかし、最終的な利子の支払総額は元金均等返済の方が30万円も安くなっています。
これは元利均等返済は月々支払額固定のところ、元金均等返済では徐々に利子分が減ることで、月々の支払い額が減り、16年目くらいで元利均等返済よりも安くなるからです。
※ 詳しくは Spread Sheet サンプル でご確認ください。
この金額をどう見るかは人それぞれかと思います。
例えば、資産運用で住宅ローンの借入金利よりも高い利回りを出せるのであれば、
元金均等返済で序盤からハイペースで返済を行わず、元利均等返済でゆっくり返していく方がよいという考え方もあります。
Spread Sheet サンプル
上記シミュレーションをSpreadSheetで計算してみました。
コピーして使ってみてください。
使い方
1. コピーする
上記リンクのファイルには編集権がないので、コピーして編集可能な自分のファイルを作成してください。
「ファイル」→ 「コピーを作成」をクリックします。
必要に応じて名前を変更して、「OK」をクリックします。
2. 値を変える
自分のファイルとしてコピーができたら編集ができます。
黄色くなっている「借入額 X」「金利(年利)」「ローン年数」の部分を変更してみます。
※黄色以外の部分をいじると正しい表示じゃなくなる可能性があります。
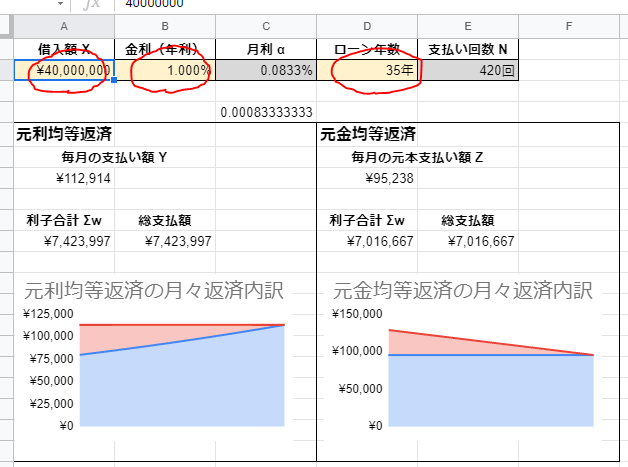
3. 計算結果を見てみる
黄色い部分の値を変更すると、計算結果が更新されます。
「元利均等返済」「元金均等返済」のそれぞれのシートがあるのでそちらで月々の支払額などを確認できます。

おわりに
ここまでいくつかの記事に渡って文字式で計算してきた結果に実際の数字をいれて返済シミュレーションを行ってみました。
検索して出てくる住宅ローンシミュレーターなどを使えば同じ結果が出てくるわけですが、その仕組みを知っておくというのも悪くないんじゃないでしょうか。(良いものですよね?)
何か誤っている点等あればご指摘いただけると幸いです。



コメント